Zufallsschwingungen – kleinere Anmerkungen zu einem disziplinverbindenden Spannungsfeld zwischen Theorie und Praxis
Viele Namen für eine Gruppe von Schwingungen
Ingenieur*innen verstehen unter Schwingungen Vorgänge, bei denen sich die betrachteten Größen im Verlaufe der Zeit ändern. Dabei wird unterschieden, ob sich derartige Prozesse eineindeutig mit mathematischen Funktionen definieren oder ob sich das Vorhandensein und die Eigenschaften der Prozessvariablen nur mit Hilfe der Wahrscheinlichkeitsrechnung beschreiben lassen. Während im ersten Fall von deterministischen Schwingungen gesprochen wird, kennzeichnet der zweite Fall die Gruppe der Zufallsschwingungen, die hinsichtlich ihres Verlaufs üblicherweise in stationäre und instationäre Prozesse unterteilt werden. So vielfältig, wie das Auftreten von Zufallsschwingungen in der Technik ist – man denke an zufällige Unebenheiten auf Verkehrswegen mit Kopfsteinpflaster, die Eigendynamik von Wandlerkarten oder den im Flug auf die Kabine einwirkenden turbulenten Lärm der Grenzschicht – so vielfältig sind auch die in der Technik gebräuchlichen Bezeichnungen für Zufallsschwingungen, die auch als stochastische Schwingungen, Rauschen, Noise oder Random Vibrations benannt werden. Die in der Praxis tätigen Ingenieur*innen sind in jedem Fall mit ihnen befasst – entweder direkt oder in der Bewertung der Frage, ob die betrachteten Nutzsignale einen ausreichend hohen Abstand zum Hintergrundrauschen aufweisen.
Die Theorie – viel Mathematik und zwei wichtige Annahmen für die Praxis
Wer in die Welt der Zufallsschwingungen eintaucht, wird sich mit praktischer Mathematik befassen. Eine Charakterisierung von Zufallsgrößen (Häufigkeit ihres Auftretens, Anzahl des Überschreitens von Grenzwerten, Verteilung von Eigenschaften innerhalb einer oder mehrerer Realisierungen) ist ohne Elemente der Wahrscheinlichkeitsrechnung nicht denkbar. Gleichermaßen werden aber vertiefte Kenntnisse der Analysis benötigt. Dies gilt insbesondere, wenn im Rahmen der Systemanalyse das Übertragungsverhalten technischer Systeme zu beschreiben ist oder für die Signalanalyse mit Hilfe von Integraltransformationen vom Zeit- in den Bildbereich gewechselt wird. Für die praktische Anwendung von Zufallsschwingungen im Ingenieurwesen sind zwei vereinfachend wirkende Annahmen von besonderer Bedeutung. Die Erste betrifft die Unterteilung von Zufallsschwingungen in stationäre und instationäre Prozesse. Sie besagt, dass Zufallsschwingungen genau dann im sogenannten weiteren Sinne als stationär betrachtet werden, wenn sich sowohl Mittelwert als auch Varianz (beide werden zur Charakterisierung verwendet) konstant sind. Die zweite Annahme ist für die praktische Anwendung unerlässlich und besagt, dass die für jeweils den selben Zeitpunkt unter Berücksichtigung ausreichender Realisierungen eines Zufallsprozesses durchgeführte Mittelung (Ensemblemittelung) einer Zufallsgröße durch die zeitliche Mittelung dieser Zufallsgröße unter Verwendung einer einzelnen, jedoch hinreichend langen, Realisierung dieses Zufallsprozesses ersetzt werden kann. Diese Annahme ist als Ergodentheorem bekannt und Grundlage für die praktische Anwendung von Zufallsschwingungen.
Die Anwendung von Zufallsschwingungen – viele Vorteile, aber auch einige Stolpersteine
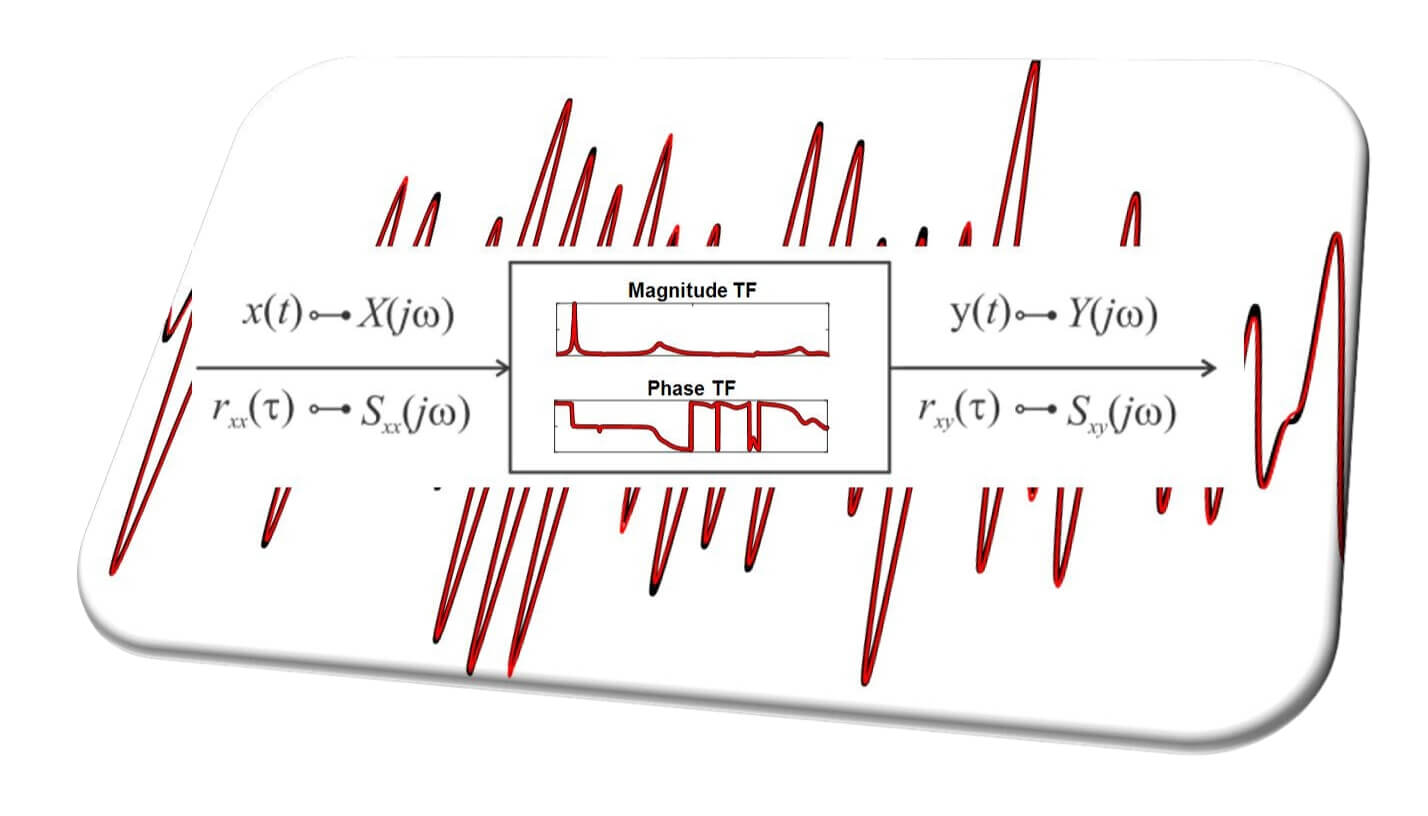
Anwendung der Theorie der Zufallsschwingungen bietet insbesondere in der Schwingungsmesstechnik zahlreiche Vorteile. Beispielsweise ermöglicht die Autokorrelationsanalyse die Wiedererkennung von Nutzsignalen, die durch ein nicht-korreliertes Rauschen maskiert sind. In der Schätzung von Übertragungsfunktionen wird ebenfalls von der Autokorrelation Gebrauch gemacht, wenn bei der Verwendung des sogenannten H1-Schätzers nicht-korrelierte Störungen im Sensorsignal (am Systemausgang) unterdrückt oder mit Hilfe des sogenannten H2-Schätzers nicht-korrelierte Störungen im Systemeingang reduziert werden. Die Anregung eines schwingungsfähigen Systems mit einer Zufallsschwingung ermöglicht sowohl die Anregung eines breiten Frequenzbandes (was hilfreich ist, um die Dauer der Messung zu reduzieren) als auch das Erreichen eingeschwungener Zustände, da die Einhaltung des Ergodentheorems eine hinreichend lange Messung erfordert und somit dem System auch hinreichend lange Energie zugeführt wird.
Eine gewisse Vorsicht ist jedoch angebracht, wenn die Vorkenntnisse über zu untersuchende Systeme gering sind. Beispielsweise ist nicht unmittelbar einsichtig, ob bei der stochastischen Anregung eines Frequenzbandes unter Umständen nichtlineare Systemeigenschaften angesprochen werden. Dies betrifft auch die Frage, wie die Energie des Eingangssignals zu justieren ist, um durch Anregung von im zu untersuchenden Frequenzband möglicherweise vorhandenen Resonanzeffekten keine Gefahr für den Prüfling ausgehen zu lassen. Weiterhin dürfen Einzelereignisse im Zufallssignal nicht außer Acht gelassen werden, für deren Charakterisierung sich der sogenannte Scheitel-Faktor als Verhältnis von Betragsmaximum zu Effektivwert anbietet. Wer diese Vorsicht walten lässt, findet in der praktischen Anwendung von Zufallsschwingungen eine effiziente Methode zur Bestimmung von Impuls- und Frequenzantworten oder modaler Parameter. Aus der Sicht von Hochschullehrer*innen bieten Veranstaltungen zu Zufallsschwingungen nicht zuletzt eine sehr gute Möglichkeit, Studierende unterschiedlicher Fachdisziplinen anzusprechen. Dies gilt beispielsweise für Kurse zur aktiven Lärmminderung, die an der Fakultät für Technik und Informatik der HAW Hamburg seit März 2012 im Studiengang Mechatronik (B.Sc.) angeboten werden.